Poďme sa pozrieť, aký ma vlastne predpis táto rovnica.
Poďme si vysvetliť, čo tie písmena vlastne znamenajú:
a,b,c sú parametre - väčšinou zadané
x - je premenná alebo neznáma, ktorú máme vypočítať
parameter a musí byť rôzny od nuly
ostatné parametre b,c môžu byť rôzne
Poznámka: ak by sa parameter a rovnal nule, potom by to už nebola kvadratická rovnica pretože:
Kvadratická sa nazýva práve kvôli členu 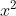
Najjednoduchšia kvadratická funkcia vyzerá takto , 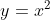
_________________________________________________________________________
Zložitejšia kvadratická funkcia by mohla vyzerať:
______________________________________________________________________
Ako menia dané parametre vzhľad kvadratickej funkcie?
Poďme sa riadiť predpisom: 
Parameter a
-rozhoduje o strmosti krivky, čím väčší parameter, tým funkcia rýchlejšie "vystrelí" do hora. Ak je parameter menší, funkcii sa "vystrelí" pomaly.Každopádne, hovoriť o tom či je parameter a veľký alebo malý je subjektívna záležitosť, preto si poďme na jednoduchej funkcii
Pre jednoduchosť zvolím za prvý parameter 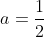 a potom
a potom 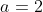
Ak je parameter a kladný, funkcia má minimum vo vrchole.
Krivka kladného parametra a pripomína usmievavého smajlíka
Krivka záporného parametra a pripomína mračiacého sa smajlíka

Parameter b
- rozhoduje o posune krivky naľavo alebo napravo po osi x
- rozhoduje o vzdialenosti medzi koreňmi (ak sú)
Parameter c
- rozhoduje o posune krivky hore alebo dole po osi y
Rozklad kvadratickej rovnice na "štvorec"
Kedže sa to slovami opisuje veľmi ťažko, ukážeme si to na nasledujúcom príklade:


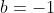


KROK Č.1
pred 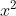 musíme mať vždy 1
musíme mať vždy 1
v tomto prípade tam jednotku nemáme, musíme vyňať 2 pred zátvorku
POZOR! nikdy nie deliť rovnicu dvomi!!!
KROK Č.2
pričítame a znovu odčítame druhú mocninu polovice parametra b
Takže urobíme toto:
polovica z b je
umocníme na druhú 
Dostali sme číslo 
KROK Č.3
Teraz ideme toto číslo pričítať a znova odčítať do rovnice
vidíme, že čísla sa nám vynulujú a teda nič sme v rovnici nepokazili
KROK Č.4
predošlí krok sme urobili z jedného dôvodu. A to z toho, aby sme dostali vzorec 
resp. 
V tomto prípade, hneď na začiatku máme výraz
Tento výraz si vieme zapísať ako:
KROK Č.5
Pokračujeme s úpravami. Dostali sme:
Vnútro zátvorky si trochu upravíme :
KROK Č.6
Roznásobíme zátvorku
upravíme
Dámi a Páni, nájdeme x-ový a y-ovú zložku vrchola :
x-ová sa nachádza v zátvorke, pýtam sa : Čo musím dosadiť za x aby zátvorka vyšla 0 ?
Jediné možné riešenie pre x: je
Ďalej hľadáme y-ovú zložku vrchola. Na konci nám ostalo číslo. Toto je číslo, ktoré hľadáme:
Takže ZÁVER: Vrchol má súradnice




