Neurónové siete
--Artificial neural network--
Prečo
Keď som sa pokúšal pochopiť celé fungovanie tejto mašinérii, strávil som nespočetne veľa človekohodín hľadaním informácií, ktorých na SR stránkach nebolo bohvie-ako veľa.
V prvom rade som sa pokúšal brázdiť wikipédiou, prečítal som si históriu, základné fungovanie a zopár ďalších dodatočných informácií. Kedže som programátorom, chcel som si svoju neurónovú sieť naprogramovať sám. Až po chvíli som ale zistil, že nič vlastne neviem a že celá moja predstava nebola ucelená a jasná!
Po zopár dalších hodinách strávených na weboch a pdf-dokumentoch som si už povedal, že teraz už tomu snáď konečne rozumiem. CHYBA, nerozumel.
S čím bol problém? S vedecky podanými informáciami. Ale to je v poriadku, je to vskutku všeobecný problém, kedže každý vedec potrebuje mať všetko odvodené korektne a matematicky správne.
Ľudia vedia robiť iba niečo, čoho princíp chápu úplne presne a na pochopenie princípu potrebujú stručné a laicky podané informácie, ktoré daný princíp vysvetlia.
V ďalších riadkoch sa pokúsim laicky sformulovať základy a možno aj pokročilejšie veci k neurónovým sieťam.
Čo to sú neurónové siete ?!
Teoretická definícia: Umelá neurónová sieť je výpočtovo-dátový model, založený na báze fungovania biologických neurónových sietí. Informácie v neurónovej sieti sú reprezentované číselnou podobou v tzv. váhach, ktoré spájajú neuróny. (1 váha spája 2 neuróny).
Váha - reprezentuje akúsi hrúbku spojenia. MATEMATICKY popisuje, ako dôležité je prepojenie medzi spájanými neurónami. V ľudskom mozgu sa nachádza až 30 miliárd neurónov. Každý z nich nie je v spojení. V umelých neurónových sieťach reprezentujeme "žiadne" spojenie ako nulovú váhu spájajúce dva neuróny. Existujú ale aj také architektúry, kde spojenia aj v čiselno-váhovom prepojení zanikajú a znova vznikajú (tu sa tým zaoberať nebudem).
Váha - reprezentuje akúsi hrúbku spojenia. MATEMATICKY popisuje, ako dôležité je prepojenie medzi spájanými neurónami. V ľudskom mozgu sa nachádza až 30 miliárd neurónov. Každý z nich nie je v spojení. V umelých neurónových sieťach reprezentujeme "žiadne" spojenie ako nulovú váhu spájajúce dva neuróny. Existujú ale aj také architektúry, kde spojenia aj v čiselno-váhovom prepojení zanikajú a znova vznikajú (tu sa tým zaoberať nebudem).
ALE AJ TAKTO!
tu sa pochopiteľne nejedná o umelú sieť ;)
Základný model
Najjednoduchšia NS vyzerá takto:
Popis:
Čierne guličky a posledná biela gulička -> to sú NEURÓNY
x1 ⟶ prvý vstup ( vstupný neurón)
x2 ⟶ druhý vtup ( vstupný neurón)
w1 ⟶ váha krorá vedie z prvého neurónu do posledného neurónu
w2 ⟶ váha ktorá vedie z druhého neurónu do posledného neurónu
y ⟶ výstup (výstupný neurón)
Vstupy v neurónoch sú čísla. Napriklad 0,1, 0.3 , 2012 , 3.14159265358979 , 500000000
Vstup musí byť číslo. (alebo číselná reprezentácia niečoho ⟶ dostanem sa k tomu neskôr)
Ako funguje neurónová sieť?
Neurónová sieť, ďalej ako NS.
NS má aspoň jeden vstup a aspoň jeden výstup.
Zakladný princíp fungovania je, laicky povedané ⟶ Do NS vstupuje číslo (čísla) a vystupujú čísla. Podobne ako v matematických funkciách, majme funkciu y=x2. Do funkcie vložíme číslo 5 a ako výstup dostaneme číslo 25. Podobne si predstavíme aj neurónovú sieť. Predstavme si to ako magickú kocku s dvoma dierami. Jedna diera na vrchu, ktorá príjma čísla. Niečo sa v tej kocke stane a druhou dierou dostaneme výstup.
Napríklad:
- dajme do NS 2 vstupy, napríklad "Vonku prší" a "Je pondelok" a naša NS nám má predpovedať číslo od 0-10, ktoré znázorňuje našu momentálnu náladu.
Vyššie som spomínal, že do NS musí vstupovať číselná reprezentácia, ale ja tu mám nejaké vety ako "vonku prší" a "je pondelok", preto musíme tieto výrazy - vety, reprezentovať číslami.
Takže prvá veta reprezentuje počasie, budeme reprezentovať počasie následovne:
-1 = prší
0 = zamračené
1 = pekne
ďalej si reprezentujeme deň v týždni ako číslo, napriklad pondelok = 0, utorok = 1 atď...
Takže do NS nám podľa viet "Vonku prší" a "Je pondelok" vstúpia čísla -1 a 0
Teraz máme číselnú reprezentáciu a neurónová sieť nám bude schopná povedať alebo predpovedať na aké číslo sa cítime. 0 - zle, 10 - veľmi dobre - Alebo do NS budeme vstupovať 40 000 vstupmi, ktoré budú číselná reprezentácia pixelov - pixely sú v skutočnosti tiež čísla.
Na základe týchto pixelov na fotke nám NS povie či sa jedná na fotke o mačiatko alebo sa nejedná o mačiatko - Ostatné príklady si nechám na neskôr, dva vyššie uvedené príklady som chcel uviesť len ako naozaj uvedenie príkladov čo NS dokážu.
FEEDFORWARD
Lepší, pre vás zrozumiteľnejší výraz by bol dopredné šírenie, alebo šírenie signálu DOPREDU, šírenie signálu "z ľava doprava" .
Čo máme: Vstupy - OK
Čo sa deje: V začiatočných neúrónoch sa momentálne nachádzajú čísla, tieto sa posunú dopredu tým, že sa vynásobia váhami, ktoré spájajú daný neurón, násobené číslo sa pripočíta k číslu v ďalšom neuróne na konci váhy.
PRIKLAD Č.1
Takže povedzme, že máme 2 vstupné neuróny a 1 výstupný neurón.1. vstup = 3
2. vstup = 2
1. vaha = 1
2. vaha = 2
V poslednom neuróne je momentálne hodnota 0 (NULA).
Poznámka: v každom neuróne na začiatku simulácie je suma 0. Až po prechodoch signálov sa sumy zväčšujú.
posledný neurón bude mať hodnotu x1 * w1 + x2 * w2
takže 3*1 + 2*2 = 7
Posledný neurón bude mať hodnotu 7.
Povedzme že máme túto jednoduchú NS. V tomto prípade sme použili jednoduché matematické operácie.
Pri zložitejších arcitektúrach sa objavia už elegantnejšie veci.
V neurónoch sa objavia tzv. aktivačné funkcie, ktoré premenia vstup z neurónu a pošlú ďalej signál, ktorý najprv prejde aktivačnou funkciou.
Typy aktivačných funkcii:
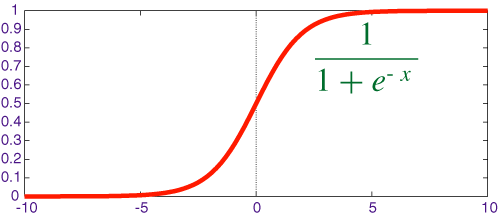
V tomto prípade, vstupuje číslo 7, podľa vzorca neurón odošle ďalej číslo : 0.9990889
Poznámka: v každom neuróne na začiatku simulácie je suma 0. Až po prechodoch signálov sa sumy zväčšujú.
posledný neurón bude mať hodnotu x1 * w1 + x2 * w2
takže 3*1 + 2*2 = 7
Posledný neurón bude mať hodnotu 7.
Povedzme že máme túto jednoduchú NS. V tomto prípade sme použili jednoduché matematické operácie.
Pri zložitejších arcitektúrach sa objavia už elegantnejšie veci.
V neurónoch sa objavia tzv. aktivačné funkcie, ktoré premenia vstup z neurónu a pošlú ďalej signál, ktorý najprv prejde aktivačnou funkciou.
Typy aktivačných funkcii:
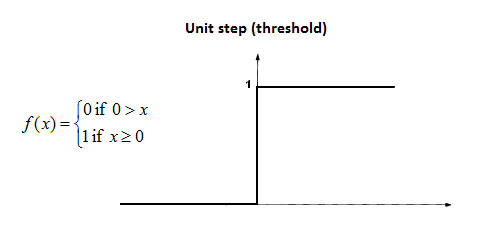
- Treshold
- Sigmoid
- ArcusTangens
- Linear
Budem pokračovať s predošlým príkladom, kde sme v poslednom neuróne dostali sumu 7
Treshold: ak hodnota>0 tak pošli dalej 1, inak pošli ďalej 0
V tomto prípade ak vstupuje číslo 7, neurón odošle hodnotu 1.
V tomto prípade, vstupuje číslo 7, podľa vzorca neurón odošle ďalej číslo : 0.9990889
Linear:
Sumu pošle dalej, nemení ju. Napríklad vstup je 7, tak pošle ďalej hodnotu 7.Používajú sa aj dalšie typy aktivačných funkcií, ktoré tu nebudem ďalej rozoberať. Tie najdôležitejšie som popísal ! :)
ZOPAKOVANIE:
Aktivačné funkcie sa nachádzajú v neurónoch ( vo všetkých okrem vstupných )
Premieňajú vstupujúcu sumu na vystupujúcu hodnotu, podľa toho aká aktivačná funkcia sa nachádza v neuróne.
Skúsme 1 a 1
f( -1.5*1 + 1*1 + 1*1 ) = 0.5 ⟶ suma je väčšia ako 0, takže výstupom je 1.
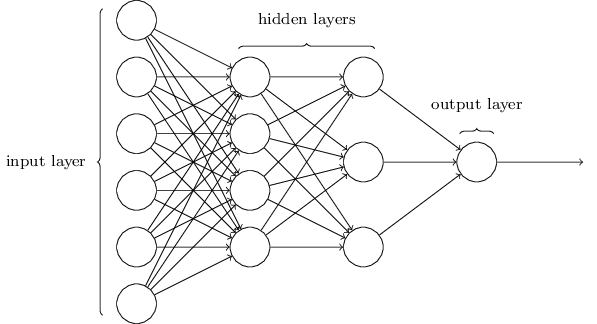
HIDDEN LAYERS - SKRYTÉ VRSTVY
Zatiaľ sme sa stretli s tým, že NS mala iba niekoľko vstupov ( inputov ) a jeden output neurón.
V skutočnosti môže mať veľmi veľa vstupných a výstupných neurónov.
Vertikálne začlenenie neurónov nazývame VRSTVA.
Ak máme n výstupných neurónov, všetky tieto výstupné neuróny sa nachádzajú vo výstupnej vrstve.
Analogicky vstupné neuróny sa nachádzajú na vstupnej vrstve.
Medzi vstupnou a výstupnou vrstvou sa môžu nachádzať skryté vrstvy.
Tieto vrstvy takisto obsahujú niekoľko neurónov.
UČENIE S UČITEĽOM
Vyššie sme si ukázali príklad s Feedforwardom, alebo dopredným šírením signálu. Do siete sme vložili vstupy a dostali sme (nejaké) výstupy.
Ako to funguje u človeka, keď sa narodí. Zatiaľ nepozná okolitý svet a jeho fungovanie. Ale nemôžeme povedať, že nemá v hlave nič. Práve naopak, jeho mozog a jeho neuróny sú bohato pospájané, ale spojenia zatiaľ nedávajú význam.
Až keď sa človek postupne učí, tie správne neuróny sú spojené s ostatnými ďalšími v správnej kombinácií, čím vytvárajú komplexnosť a celkovo "začnú ťahať za jeden povraz" .
Analogicky v našej umelej neurónovej sieti máme na začiatku neuróny. Povedzme aj, že každá vrstva je poprepájaná s ďalšou nasledujúcou. Sú tam síce prepojenia, ale každé prepojenie má náhodnú, ľubovoľnú váhu a dokopy tvorí sieť iba komplex chaosu.
Na to aby sa sieť niečo naučila, potrebujeme ju učiť na istých príkladov (examples).
Z názvu - učenie s učiteľom ⟶ vyplýva, že ak NS urobí niečo zle, vieme jej povedať, čo spravila zle.
Napríklad NS nám dala na výstupe číslo 10, ale mala dať číslo 15. Tak jej povieme "pomýlila si sa o 5". Následne je schopná sa naučiť danú vec urobiť lepšie, aby nabudúce, čo možno presnejšie, na výstupe podala číslo bližšie k 15.
To akým spôsobom sa NS učí popíšem až v nasledujúcej časti.
BIAS
Je špeciálny optimalizačný TYP neurónu, ktorého výstupom je vždy číslo 1.
Z toho vyplýva, že nezáleží na tom, čo sa do tohto neurónu dostane ako súčet (suma), výstup alebo output bude vždy hodnota 1.
Logicky z toho taktiež vyplýva, že do BIAS neurónu nesmeruje žiadna váha, ani nie je "zozadu" spojený s neurónami.
Dopredu je ale poprepájaný klasicky.
Príklad jednoduchej neurónovej siete na príklade BOOLEAN hodnoty AND
Toto je tabuľka hodnôt AND
Našou úlohou bude nájsť NS, ktorá nám zo vstupov A a B vyhodnotí výstup Y, ktorý sa bude rovnať A AND B. (tak ako v tabuľke)
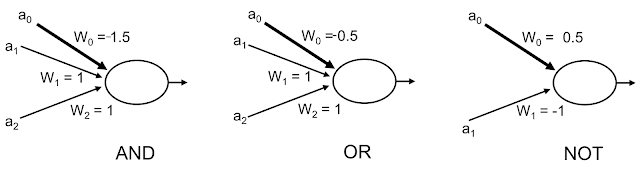
Pre tento problém neuronová sieť vyzerá takto:
AND funkcia prvý zľava, ďalej ALEBO, a nakoniec negácia
! ešte doplním, že výstupné neuróny využívají treshold aktivačnú funkciu !
PRÍKLAD:
skúsime si príklad NS funkcie AND.
Dosadíme si hodnoty napríklad 0 a 1.
a0 = toto je BIAS = vždy 1
a1 = 0
a2 = 1
suma v poslednom neuróne = -1.5 * 1 + 0 * 1 + 1*1 = f(-0.5) = 0
f( nieco ) - je aktivacna funkcia, do ktorej vstupuje ako argument suma okolitych neuronov
kedže aktivačná funkcia bola treshold, tak -0.5 je menšie ako 0 takže výstupom je 0.
ako vidíme 0 A 1 = 0 PRAVDA...Skúsme 1 a 1
f( -1.5*1 + 1*1 + 1*1 ) = 0.5 ⟶ suma je väčšia ako 0, takže výstupom je 1.
! Skúste to overiť aj pre ďalšie boolean funkcie z obrázka !
V ďalšej časti sa dozviete, ako nastaviť, alebo naučiť váhy tak, aby nám spolu dávali to čo chceme.