Math and IT: 2016

Definícia: Derivácia je matematické vyjadrenie ZMENY niečoho.

Na výpočet derivácie potrebujeme 2 body, medzi ktorými bude zmena vypočítaná.

Vzorec:

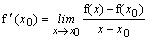
Predstavme si 2 body A a B, ktoré sú od seba vzdialené dĺžkou Δx.

Ak ich spojíme priamkou, vznikne nám medzi osou x a priamkou uhol Alfa.

Teraz začneme postupne približovať bod B smerom k bodu A.

Postupne bod B bude tak blízko A, že hovoríme, že sa priblížil nekonečne blízko k bodu A.

Takže medzi bodom A a B existuje nekonečne malá vzdialenosť Δx.

Tieto nekonečne blízke body opäť spojíme priamkou. Vznikne nám dotyčnica k funkcií f(x) v bode A.

Tg(Alfa) = derivácia v bode A.

Mohol by som pokračovať ďalej v týchto teoretických veciach, každopádne, toto sú veci, ktorým sa študenti venujú menej a zaujímajú ich iba vzorce na derivácie, aby to mohli vedieť na písomku a podobne. V tejto sekcií teda nebudem pokračovať v teorií, ale skúsim vysvetliť deriváciu na ľahších príkladoch.

VZORCE NA DERIVOVANIE:

Vzťahy súčet,odčítanie,násobenie a delenie

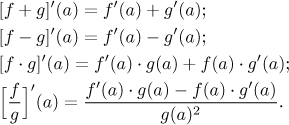
Reťazové pravidlo:

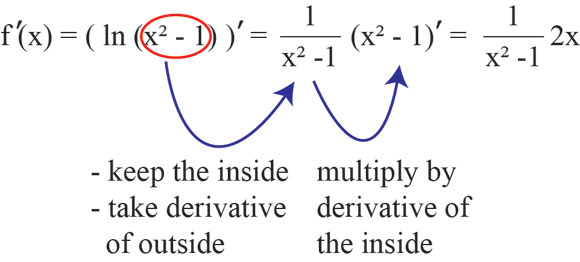
PRÍKLAD Č.1

Zderivuj y = 2x

vzorec: $(cx^n)' = c.n.x^{n-1}$

V tomto prípade je c=2 , n=1 , pretože x je vlastne x na prvú.

Dosadíme a získame -> $2.1.x^0 = 2$

Výsledok: y' = 2

PRÍKLAD Č.2

Zderivuj y = 6

Vzorec (c)' = 0

Vysvetlenie: Derivácia konštanty je nula.

Výsledok , y' = 0

PRÍKLAD Č.3

Zderivuj $y=x^6$

Vzorec: $y=x^n ... potom \rightarrow y' = n\cdot x^{n-1}$

Výsledok $y' = 6x^5$

PRÍKLAD Č.4

Zderivuj $y=(x+1)^2$

Tento krát je tu nový príklad, ktorý sa ráta trochu iným spôsobom. Najprv sa celá zátvorka (x+1) zoberie akoby to bola jedná neznáma.

Dajme tomu, že tú zátvorku dáme do substitúcie za C.

Potom naša rovnica vyzerá ako $y=C^2$

To už sa podobá na vzorec.

Derivujeme a dostaneme $y=2C$ .

Teraz musíme vrátiť za C pôvodný výraz. Potom celú rovnicu musíme ešte vynásobiť zderivovaným Cčka. !!! Toto sa nazýva pravidlo zreťazenia.

Takže $y=2.C.C'$

$y = 2(x+1).C'$

$C = x + 1$ .... $C'=1$

takže výsledok je

$y=2(x+1)$

PRÍKLAD Č.5

Zderivuj $y=2x^2 + x + 1$

Čísla v súčte môžeme derivovať zvlášť. To znamená že 2x^2 , x a 1 derivujeme zvlášť.

Výsledok:

$y=2\cdot 2x^1 + 1\cdot x^0 + 0$

$y= 4x + 1$

PRÍKLAD Č.6

$y=-x-1$

Berieme to ako $y=-1x-1$

Takže opäť parameter pri neznámej opíšeme, neznámu derivujeme , a derivujeme aj konštanu -1 čo je 0.

Takže výsledok: $y'=-1$

PRÍKLAD Č.7

$y=\frac{1}{x}$

Na delenie síce existuje vzorec, ALE! môžeme si tento príklad prepísať TAKTO:

$y=x^{-1}$

A tento prípad sa derivuje oveľa ľahšie ako delenie.

$y=x^n$ z toho derivácia -> $y=nx^{n-1}$

Výsledok:

$y'=-1x^{-2}$

po úprave

$y'= -\frac{1}{x^2}$

PRÍKLAD Č.8

$y=\frac{5}{x^2}$

prepis na $y=5x^{-2}$

Z toho $y'=-10x^{-3}$

Po úprave

$y'=\frac{-10}{x^{3}}$

PRÍKLAD Č.9

$y = 2^x$

Vzorec: $y = a^x$ potom $y'= a^x \cdot ln{a}$

Výsledok: $y'= 2^x\cdot ln{2}$

PRÍKLAD Č.10

$y=x.ln(x)$

použijeme pravidlo derivovania SÚČIN (prve)'.druhe + prve.(druhe)'

$y=x'.ln(x)+x.(ln(x))'$

$y = 1.ln(x) + x.\frac{1}{x}$

Po úprave:

$y = ln(x) + 1$

Alebo aj : $y = ln(x) + ln(e)$ a z toho potom $y = ln(e.x)$

PRÍKLAD Č.11

$y = \frac{x^2}{ln(x)}$

Použijeme vzorec pre delenie

$y = \frac {(x^2)'\cdot ln(x) - x^2\cdot (lnx)'}{(ln(x))^2}$

Z toho

$y=\frac{2x\cdot ln(x) - x^2\cdot \frac{1}{x}}{(lnx)^2}$

Po úprave

$y=\frac{2x .ln(x) - x}{(lnx)^2}$

Alternativny tvar:

$y'=\frac{x\cdot (2.ln(x) - 1)}{(ln^2x)}$

PRÍKLAD Č.12

$y=x.e^x$

Použijeme najprv vzorec na násobenie

$y=(x)'.e^x + x.(e^x)'$

Z toho

$y=1.e^x + x.(e^x.ln{(e)})$

Po uprave: (Vysvetlenie: ln(e) = 1 )

$y=e^x+x.e^x$

Alternativny tvar: **Vyberieme e^x pred zatvorku**

$y=e^x(1+x)$

PRÍKLAD Č.13

$y=(2x^2 + x)^5$

Prv vidíme v zátvorke polynóm, ten ale nemôžeme začať derivovať kým nevyriešime vyššiu vrstvu, a to celú zátvorku umocnenú na piatu.

Takže riešime najprv mocninu.

$y=5(2x^2 + x)^4$

a teraz musíme použiť reťazové pravidlo. vynásobiť zderivovanou zátvorkou.

$y={5(2x^2 + x)^4 } \cdot(2x^2+x)'$

Výsledok:

$y={5(2x^2 + x)^4 } \cdot(4x+1)$

Math and IT

Stránky

streda 6. apríla 2016

Derivácia funkcie

VZORCE NA DERIVOVANIE:

Vzťahy súčet,odčítanie,násobenie a delenie

Reťazové pravidlo:

PRÍKLAD Č.1

PRÍKLAD Č.2

PRÍKLAD Č.3

PRÍKLAD Č.4

PRÍKLAD Č.5

PRÍKLAD Č.6

PRÍKLAD Č.7

PRÍKLAD Č.8

PRÍKLAD Č.9

PRÍKLAD Č.10

PRÍKLAD Č.11

PRÍKLAD Č.12

PRÍKLAD Č.13